A sparse MPC solver for walking motion generation (old version).: Notes on implementation

Representation of matrices

Note, that parts of state and control matrices (Model of the system) corresponding to x and y coordinates are identical. This property is preserved in all subsequent transformations, hence there is no need to compute and store all elements of static matrices (Cholesky factor for example). Consequently, we mainly operate on 3x3 matrices, which are stored in the following way:

  0   3   6
  1   4   7
  2   5   8

Cholesky factor

The Cholesky factor consists of two parts:

A constant and well structured 'upper' part, which corresponds to equality constraints:

           full L                           |   compressed L
            a                               |
            0   a                           |           a
            b   0   c                   0   |           b   c
            0   b   0   c                   |   ===>        d   e
                    d   0   e               |   ===>            f   g
                    0   d   0   e           |                       ...
                0           f   0   g       |
                            0   f   0   g   |
                                    ....    |

Here a,c,e,g - lower diagonal 3x3 matrices; b,d,f - upper triangular 3x3 matrices. This matrix is reffered as ecL. It is stored as a sequence of vectors of 9 elements:

        0  3  6 
        1  4  7
        2  5  8

        9  12 15  18 21 24
        10 13 16  19 22 25
        11 14 17  20 23 26

                    ...         ...

A less structured part corresponding to inequality constraints. It is altered each time the active set is changed. This part is stored as a set of 2*N vectors. The length of each vector could not be longer than N*SMPC_NUM_VAR.

Implementing bounds

Consider the variable

$\mbm{x} = \left[\begin{array}{c} x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \\ x_6 \end{array}\right].$

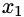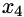Suppose that variables $x_1$ and $x_4$ have simple bounds (and the rest of the variables are are not subject to inequality constraints), i.e.,

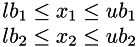
$\\ lb_1 \leq x_1 \leq ub_1 \\ lb_2 \leq x_2 \leq ub_2$

The above four inequality constraints can be written as

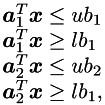
$\\ \mbm{a}_1^T\mbm{x} \leq ub_1 \\ \mbm{a}_1^T\mbm{x} \geq lb_1 \\ \mbm{a}_2^T\mbm{x} \leq ub_2 \\ \mbm{a}_2^T\mbm{x} \geq lb_1,$

where

$\\ \mbm{a}_1^T = \left[\begin{array}{cccccc} 1 & 0 & 0 & 0 & 0 & 0 \end{array}\right] \\ \mbm{a}_2^T = \left[\begin{array}{cccccc} 0 & 0 & 0 & 1 & 0 & 0 \end{array}\right].$

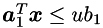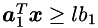Note that both $\mbm{a}_1^T\mbm{x} \leq ub_1$ and $\mbm{a}_1^T\mbm{x} \geq lb_1$ can not be in the working set at the same time (because if we are on one of the bounds we can not be on the other one).

Attention:: Note, that if we do not distinguish lower and upper bounds, Lagrange multipliers can be negative.