A sparse MPC solver for walking motion generation (old version).: Removing inequality constraints

This page describes changes in KKT system after removal of inequality constraint from the active set.

Downdate of Cholesky factor

Imagine, that we have selected an inequality constraint for removal, then corresponding line and column must be removed from matrix 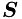$\mbm{S}$ . We can represent this by moving these lines to the end and to the right of the matrix using permutation matrix:

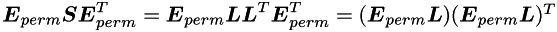
$\mbm{E}_{perm} \mbm{S} \mbm{E}_{perm}^T = \mbm{E}_{perm} \mbm{L} \mbm{L}^T \mbm{E}_{perm}^T = (\mbm{E}_{perm} \mbm{L}) (\mbm{E}_{perm} \mbm{L})^T$

But matrix 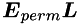$\mbm{E}_{perm} \mbm{L}$ is not lower triangular. We can transform it using Givens rotation matrices (which, obviously, cancel out):

    .                 .                     .                 .
    ..                ..                    ..                ..
    ...  -> remove -> .... <  -> Givens  -> ...  -> Givens -> ...
    ....     line     .....<     rotation   .....   rotation  ....
    .....               ^^^
                      these elements 
     L                must be adjusted

The rotations are performed in the following way:

from two columns, which must be updated, topmost 2x2 matrix is taken;
the rotation matrix is formed in such a way, that this 2x2 matrix becomes diagonal;
the selected two columns are multiplied by the rotation matrix.

The Cholesky decomposition is unique: given a positive-definite matrix A, there is only one lower triangular matrix L with strictly positive diagonal entries such that A = L*L'. The algorithm presented above can produce L with negative diagonal entries. If a negative diagonal element is found, the sign of the whole column must be altered after rotation.

Downdate of z

All elements of 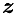$\mbm{z}$ starting from the position corresponding to the last non-zero (diagonal) element of removed row must be updated.

Consider the following situation (based on formulas derived in section 'Update of z'):

$\left[ \begin{array}{cccc} \mbm{L} & \mbm{0} & \mbm{0} & \mbm{0} \\ & \mbox{removed line} &&\\ & \mbox{ignored lines} &&\\ \mbm{l}^T & \ell_{rem} & \mbm{l}^T_u& \ell_n \end{array} \right] \left[\begin{array}{c} \mbm{z} \\ z_{rem} \\ \mbm{z}_u \\ z_n \end{array}\right] = \mbm{s}$

Some lines are not important right now and they are marked as 'ignored'. Elements of 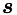$\mbm{s}$ are computed on demand and there is no need to alter it. 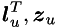$\mbm{l}^T_u, \mbm{z}_u$ must be updated. Vector 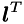$\mbm{l}^T$ is not affected by update (see section 'Downdate of Cholesky factor'). Hence the following number stays constant:

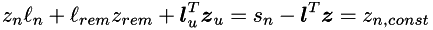
$z_n \ell_n + \ell_{rem} z_{rem} + \mbm{l}^T_u \mbm{z}_u = s_n - \mbm{l}^T\mbm{z} = z_{n,const}$

After Cholesky factor was updated we get:

$\left[ \begin{array}{ccc} \mbm{L} & \mbm{0} & \mbm{0} \\ & \mbox{ignored lines} &\\ \mbm{l}^T & \mbm{l}^T_{u,new}& \ell_{n,new} \end{array} \right] \left[\begin{array}{c} \mbm{z} \\ \mbm{z}_{u,new} \\ z_{n,new} \end{array}\right] = \mbm{s}$

The new element of vector z can be computed:

$z_{n,new} = \frac{z_{n,const} - \mbm{l}^T_{u,new} \mbm{z}_{u,new} }{\ell_{new}}$

Note, that computation of new elements 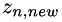$z_{n,new}$ must be started from the element corresponding to the first changed line of L and continued towards the end of z.