![$ \left[ \begin{array}{cc} 2\mbm{H} & \mbm{E}^T \\ \mbm{E} & \mbm{0} \end{array} \right] \left[ \begin{array}{c} \mbm{x}_{init} + \Delta\mbm{x}\\ \mbm{\nu} \end{array} \right] = \left[ \begin{array}{c} -\mbm{g} \\ \mbm{\bar{e}} \end{array} \right]. $](form_25.png)
Section 'Problem definition' discusses formation of matrices 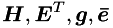 .
.
We assume, that an initial guess satisfying all constraints is given (instructions on how to generate it are given in section 'Generation of an initial feasible point') Our goal is to find delta between initial guess and optimal point. From the system presented above we can derive:
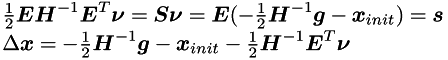
Here 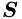 is a Schur complement, its structure is described in section 'Schur complement'.
is a Schur complement, its structure is described in section 'Schur complement'.
Note, that 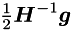 is constant and due to the structure of the matrix and vector has only 2*N non-zero elements. Also, since Hessian is diagonal its invertion is trivial and multiplication of inverted Hessian by any vector is O(N).
is constant and due to the structure of the matrix and vector has only 2*N non-zero elements. Also, since Hessian is diagonal its invertion is trivial and multiplication of inverted Hessian by any vector is O(N).
 1.8.0
1.8.0