Once Schur complement is formed we can use Cholesky decomposition 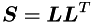 . to obtain Langrange multipliers.
. to obtain Langrange multipliers.
![$ \mbm{L} = \left[ \begin{array}{cccccc} \mbm{L}_{11} & \mbm{0} & \mbm{0} & \dots & \mbm{0} & \mbm{0} \\ \mbm{L}_{21} & \mbm{L}_{22} & \mbm{0} & \dots & \mbm{0} & \mbm{0} \\ \mbm{0} & \mbm{L}_{32} & \mbm{L}_{33} & \dots & \mbm{0} & \mbm{0} \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ \mbm{0} & \mbm{0} & \mbm{0} & \dots & \mbm{L}_{N-1,N-1} & \mbm{0} \\ \mbm{0} & \mbm{0} & \mbm{0} & \dots & \mbm{L}_{N,N-1} & \mbm{L}_{NN} \end{array} \right], $](form_51.png)
Directly from observation we have
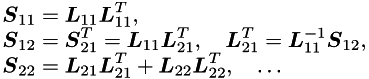
In the second step 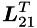 is computed by forward substitution, and in the third step, forming
is computed by forward substitution, and in the third step, forming 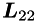 requires the computation of the Cholesky factors of
requires the computation of the Cholesky factors of 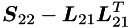 .
.
 1.8.0
1.8.0